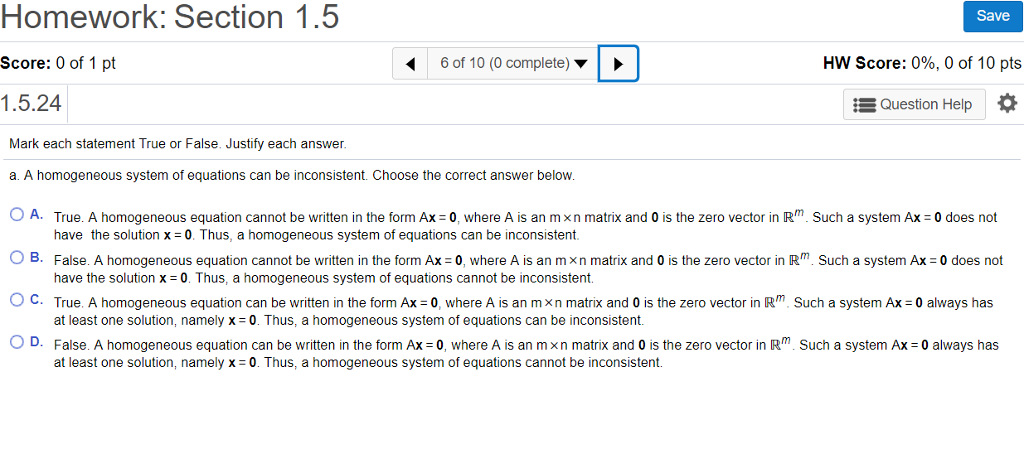
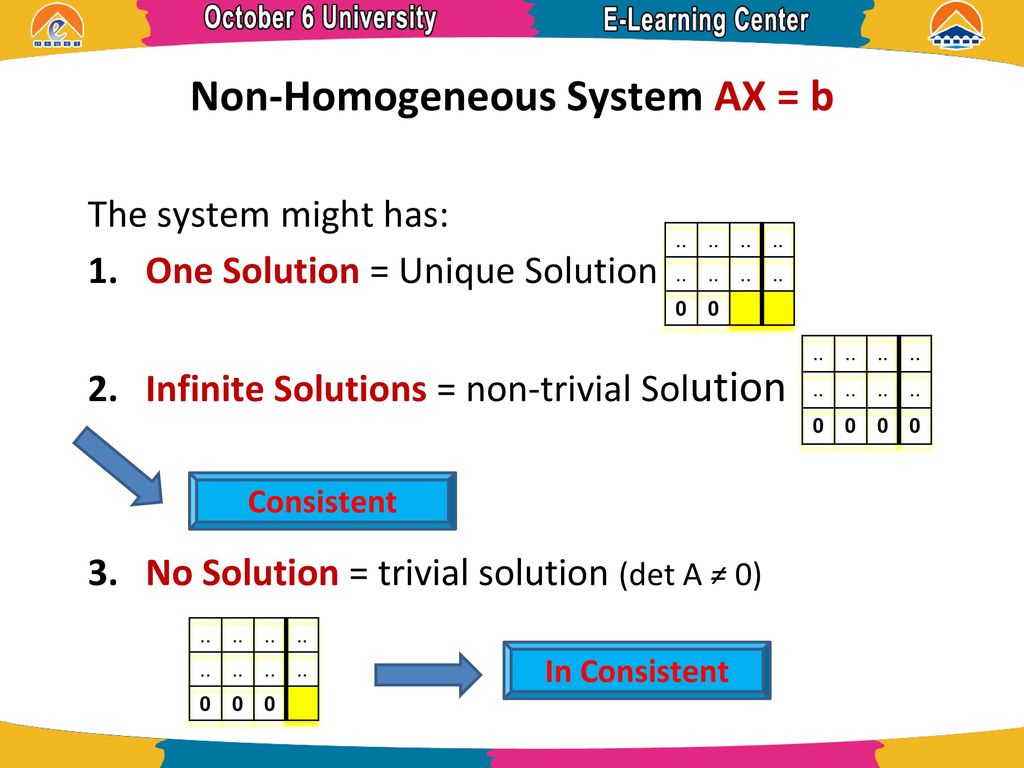
A Homogeneous System Of Equations Can Be Inconsistent
A homogeneous system of equations can be inconsistent. Ere is only one solution and that must be the trivial solution. Homogeneous system of equations is always consistent. Thus a homogeneous system of equations cannot be inconsistent.
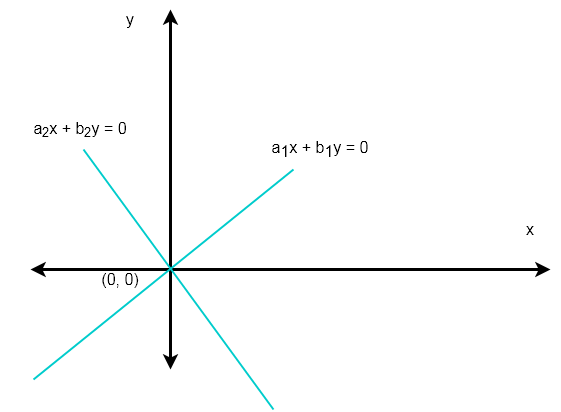
If there is NO solution and also if one deserve to derive a contradiction from equations then the system is inconsistent. A homogeneous system is always consistent. Algebraically for such a case fraca_1a_2 fracb_1b_2 fracc_1c_2 and the pair of linear equations in two variables is said to be inconsistent.
I to be not certain if i misunderstood the consistency definition. A homogeneous system is ALWAYS consistent since the zero solution aka the trivial solution is always a solution to that system. A homogeneous system always has at least one solution namely the zero vector.
Thus a homogeneous system of equations cannot be inconsistent. When a row operation is applied to a homogeneous system the new system is still homogeneous. A homogeneous equation can be written in the form Ax0 where A is an mtimesn matrix and 0.
If there are no free variables thProof. Thus a homogeneous system of equations can be inconsistent. Cook answered the mathematical definition of it would be when b lies in the Columnspace of A.
If A is a 3 x 3 matrix and if X consists of x1 x2 and x3 then putting x1 x2 x3 0 we have a solution. For example the equations. At least one solution namely x0.
C If the system of homogeneous linear equations possesses non-zeronontrivial solutions and Δ 0. Consider any homogeneous system of four linear equations and three unknowns.
You are watching.
A homogeneous system is ALWAYS consistent since the zero solution aka the trivial solution is always a solution to that system. If x is a nontrivial solution of Ax0 then every entry in x is nonzero. A homogeneous system of equations can be inconsistent. A homogeneous equation cannot be written in the form Ax-0 where A is an mxn matrik and O is the zero vector in Such a system Ax 0 does not have the solution x 0. A homogeneous system is always consistent. Since a homogeneous system always has the solution mathbfxmathbf0. So there is always a solution for homogeneous system of equations. The above system 1 can be put in the matrix form AX O m x1 where. A homogeneous system always has at least one solution namely the zero vector.
Consider any homogeneous system of four linear equations and three unknowns. I to be not certain if i misunderstood the consistency definition. Cook answered the mathematical definition of it would be when b lies in the Columnspace of A. Ere is only one solution and that must be the trivial solution. Thus a homogeneous system of equations can be inconsistent. The above system 1 can be put in the matrix form AX O m x1 where. Furthermore can a homogeneous system be inconsistent.



















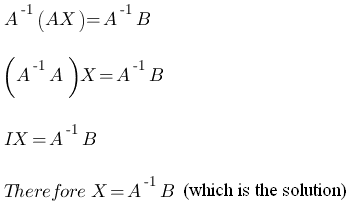






















Post a Comment for "A Homogeneous System Of Equations Can Be Inconsistent"